Series resonance quality factor? Wuhan UHV specializes in the production of series resonance, with a wide range of product selection and professional electrical testing. To find series resonance, choose Wuhan UHV. 

The quality factor in series resonance is an electrical and magnetic quantity. A quality indicator that represents the ratio of energy stored in an energy storage device (such as an inductor, capacitor, etc.) or resonant circuit to the energy lost per cycle; The Q value of the reactive element in a series resonant circuit is equal to the ratio of its reactance to its equivalent series resistance; The larger the Q value of a component, the better the selectivity of the circuit or network composed of that component. 

For non radiative systems, such as Z=R+jX, then Q=| X |/R. SI unit: 1 (one). Q=reactive power/active power, and the quality factor of a series resonant circuit is the ratio of the characteristic impedance of the series resonant circuit to the circuit resistance. In a series circuit, there are two methods for measuring the quality factor Q of the circuit. One is to determine it according to the formula Q=UL/U0=Uc/U0, where Uc and UL are the voltages on capacitor C and inductor L at resonance, respectively; Another method is to measure the passband width △ f=f2-f1 of the resonance curve, and then calculate the Q value based on Q=f0/(f2-f1). In the formula, f0 is the resonant frequency, and f2 and f1 are the upper and lower frequency points when the amplitude of the output voltage drops to 1/√ 2 (=0.707) times the maximum value due to detuning. The larger the Q value, the sharper the curve, the narrower the passband, and the better the selectivity of the circuit. When powered by a constant voltage source, the quality factor, selectivity, and passband of the circuit are only determined by the parameters of the circuit itself and are independent of the signal source.

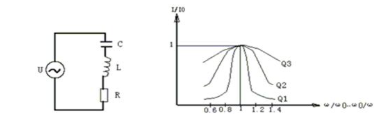
Figure 1                                                    Figure 2

Figure 1 shows a series resonant circuit consisting of a capacitor C, an inductor L, and a leakage resistance of the capacitor and a line resistance of the inductor R. The complex impedance Z of this circuit is the sum of the complex impedances of three components. Z=R+jωL+(-j/ωC)=R+j(ωL-1/ωC)　

The resistance R in the above equation is the real part of the complex number, and the difference between the inductive reactance and the capacitive reactance is the imaginary part of the complex number. We call the imaginary part the reactance, represented by X, and ω is the angular frequency of the applied signal. When X=0, the circuit is in a resonant state, where the inductive and capacitive reactance cancel each other out, i.e. the imaginary part in equation ⑴ is zero, resulting in the minimum impedance in the circuit. Therefore, the current is at its maximum, and the circuit is now a purely resistive load circuit, where the voltage and current in the circuit are in phase. When a circuit resonates, its capacitance is equal to its inductance, so the effective voltage across the capacitor and inductor must be equal. The effective voltage across the capacitor is UC=I * 1/ω C=U/ω CR=QU, and the quality factor is Q=1/ω CR. Here, I is the total current of the circuit. 

Effective value of voltage on inductor UL=ω LI=ω L * U/R=QU Quality factor Q=ω L/R

Because UC=UL, Q=1/ω CR=ω L/R

From the above analysis, it can be seen that the higher the quality factor of the circuit, the higher the voltage on the inductor or capacitor compared to the applied voltage.

Circuit selectivity: The total current of the circuit in Figure 1 is I=U/Z=U/[R2+(ω L-1/ω C) 2] 1/2=U/[R2+(ω L ω 0/ω 0- ω 0/ω C ω 0) 2] 1/2 ω 0, which is the angular frequency at which the circuit resonates. When the circuit resonates, there is: ω 0L=1/ω 0C

so I=U/{R2+[ω0L(ω/ω0-ω0/ω)]2}1/2= U/{R2+[R2(ω0L/R)2](ω/ω0-ω0/ω)2}1/2= U/R[1+Q2(ω/ω0-ω0/ω)2]1/2　

Because the total current of the circuit during resonance is I0=U/R, I=I0/[1+Q2 (ω/ω 0- ω 0/ω) 2] 1/2 has a function curve of I/I0=1/[1+Q2 (ω/ω 0- ω 0/ω) 2] 1/2. Let (ω/ω 0- ω 0/ω) 2=Y

The curve is shown in Figure 2. There are three curves here, corresponding to three different Q values, among which Q1>Q2>Q3. From the figure, it can be seen that when the external signal frequency ω deviates from the resonant frequency ω 0 of the circuit, I/I0 is less than 1. The higher the Q value, the faster the current decreases at a certain frequency offset, and the sharper the resonance curve. That is to say, the selectivity of a circuit is determined by its quality factor Q, and the higher the Q value, the better the selectivity.